Dot Product of Vectors: Explained with Formula and Examples

Posted On November 24 2021

---

In Mathematics and Physics, a vector is considered as an object having both direction and magnitude. The length of the vector indicates its magnitude while the arrow shows the direction in which is it is going as shown in the below image.

The dot product also known as the scalar product is the product of the magnitudes of the two vectors and the cosine of the angle between them.

The dot product of vectors a and b can be calculated by using the following formula.

Dot Product Formula

There are two formulas to find the dot product.

Vector Dimension

(a_i a_j a_k) ∙ (b_i b_j b_k) = (a_i ∙ b_i + a_j ∙ b_j + a_k ∙ b_k)

In this equation:

 i, j, and k refer to x, y, and z coordinates on the Cartesian plane.

Vector Magnitude

a.b = |a||b| cosθ

|a| refers to the magnitude of vector a,

|b| refers to the magnitude of vector b, and

Cos θ refers to the angle of cosine between both vectors a and b.

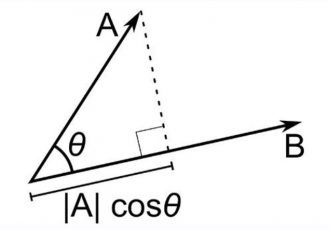
Finding Dot Product of two Vectors

You can use the dot product calculator or dot product formula to calculate the dot product of two vectors.

To find the dot (scalar) product of two vectors a and b, multiply the vectors like coordinates and then add the products together as shown in the above equation. Multiply the x coordinates of both vectors, then add the result to the product of the y coordinates. If we have vectors in three-dimensional space, we’ll add the product of the z coordinates too.

Here, we will go through a few examples to understand the calculation of dot product.

1.   Using Vectors Dimension

The following examples demonstrate the calculation of dot products using the dimension or direction of vectors.

Example 1

Vector a = (6i, 8j, 4k)

Vector b = (9i, 3j, 5k)

Place the values in the dot product formula.

(ai aj ak) ∙ (bi bj bk) = (ai ∙ bi + aj ∙ bj + ak ∙ bk)
(6   8   4) ∙ (9   3   5) = (6 ∙ 9 + 8 ∙ 3 + 4 ∙ 5)
(6   8   4) ∙ (9   3   5) = (54 + 24 + 20)
a∙b = 98

Example 2

Vector a = (2.3i, 0.9j, 5.2k)

Vector b = (0.01i, 9.027j, 0.0034k)

Place the values in the dot product equation.

(ai aj ak) ∙ (bi bj bk) = (ai ∙ bi + aj ∙ bj + ak ∙ bk)
(2.3   0.9   5.2) ∙ (0.01   9.027   0.0034) = (2.3 ∙ 0.01 + 0.9 ∙ 9.027 + 5.2 ∙ 0.0034)
(2.3   0.9   5.2) ∙ (0.01   9.027   0.0034) = (0.023 + 8.1243 + 0.01768)
a∙b = 8.2

Example 3

Vector a = (78i, 034j, 90k)

Vector b = (-67i, 45j, 98k)

Place the values in the formula.

(ai aj ak) ∙ (bi bj bk) = (ai ∙ bi + aj ∙ bj + ak ∙ bk)
(78   34   90) ∙ (-67   45   98) = (78 ∙ -67 + 34 ∙ 45 + 90 ∙ 98)
(78   34   90) ∙ (-67   45   98) = (-5226 + 1530 + 8820)
a∙b = 5124

2.   Using Vectors Magnitude

The following examples demonstrate the dot product calculation using the magnitude of vectors.

Example 1

If vector a has a magnitude of 40 and vector b has a magnitude of 60 with an angle of 30° between, what will be the dot product of vectors a and b.

Let’s use the vector magnitude formula to find dot product.

a∙b = |a||b| cosθ

Place the given values in the above equation.

a∙b = 40 × 60 × cos 30°

a∙b = 2400 × 0.866

a∙b = 2078.46

Example 2

Suppose vector |a| = 2.5 and |b| = 5.67 and θ = 20°. Calculate the dot product of a and b.

Use the vector magnitude equation to find scalar product.

a∙b = |a||b| cosθ

Substitute the given values in the above equation.

a∙b = 2.5 × 5.67 × cos 20°

a∙b = 14.175 × 0.9396

a∙b = 13.32

Example 3 – Real World Application

Find the work done if the force of 3N is exerted at an angle of 75° to the displacement of 12 meter.

As we know, the work done formula constitutes of:

W = F∙d

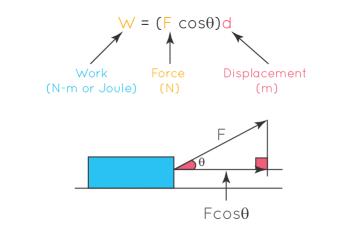
The dot product formula can be used to find the work done. If we consider force and displacement as two vectors, the work done equation can be written as:

W = F∙d cosθ

W = 3 × 12 × cos 75°

W = 36 × 0.2588

W = 9.3174 j

Properties of the Dot Product

The followings are the properties of dot product.

1. Dot product of two vectors is commutative i.e. b = b.a = ab cos θ.
2. If b = 0then it can be seen that either b or a is zero or cos θ = 0 ⇒θ = π/2. It suggests that either of the vectors is zero or they are perpendicular to each other.
3. Also we know that using scalar product of vectors (pa) . (qb) = (pb) . (qa) = pq a.b
4. The dot product of a vector to itself is the magnitude squared of the vector i.e. a.a = a.a  cos 0 = a²
5. The dot product follows the distributive law also i.e. (b + c) = a.b + a.c
6. In terms of orthogonal coordinates for mutually perpendicular vectors it is seen that i . i = j . j = k . k = 1.
7. In terms of unit vectors if a= a₁i + a₂j + a₃k and b = b₁i + b₂j + b₃k then,

a . b = (a₁i + a₂j + a₃k) . (b1^i+b2^j+b3^k)

= a₁b₁ + a₂b₂ + a₃b₃ = abcosθ

Wrapping Up

After working with various examples, you would be confident to find the dot product of two vectors with both methods i.e., magnitude or direction. In the case of direction, we need point coordinates of vectors on a Cartesian pane. On the other hand, we need magnitudes of both vectors and the cosine angle to find the scalar product using the magnitude. Either way, the result will be the same if you apply the formulas appropriately.

---